Sorting Algorithms in Software Development

Introduction:

Welcome to my article on Sorting Algorithms. My intention to call it article and not a tutorial, because I don’t want to tutor anyone, but let everyone know what I have learned so far while being a Software Developer who has given many interviews. The article is written in a hope that I will be able to explain the sorting algorithms logically and not childishly. Only assumption is that the reader is software developer enthusiast, I don’t assume he/she knows everything but just simple basics of software development. I will also put down pseudo codes as well as actual code Python code snippets that will help reader understand the algorithms better.

What?

Sorting is arranging/re-arranging given data in an ordered sequence based on certain defined criteria. Simple example is to arrange boxes from smallest to largest size or from largest to smallest size. Only one caveat to the sorting is that, the criteria on which the sorting needs to be done should be available with all the given data and also must apply to all the given data equally. For example if we want to arrange given list of employees in a company based on their salaries, every employee must have salary information.

Why?

Nothing in real life can be guaranteed to be in specific order. Almost everything is thrown at you randomly. So what do you do? You sort them out. I am a hands on Software Developer (being a MS in Mechanical Engineering) so I won’t give bookish answers but straight forward real life examples where sorting was needed. With these examples I am sure you will understand why do we need sorting at all?

Rearrange the list of 3D cells in ascending order of their geometric id’s to find out which cells lie in-front of any given cell. I know this can be done using linked list but linked list becomes expensive when traversing to access certain data.
Output the names, id’s and department of all employees sorted in ascending order according to their names.
In a calendar week there can be several breaks in working hours for a factory. Each break has start time, end time and day of the week as parameters. So when a task is to be done that spans across two days we will need to split the task to get several tasks so that there will be no work done during breaks. How would you find out which break is next? Answer is sorting the breaks according to day of the week and then by start times
Find the top 10 songs of the week based on the views or top 50 companies based on the revenue

I can give more examples like these from FEA (Finite Element Analysis), CFD (Computational Fluid Dynamics) and CAD (Computer Aided Design)

How?

Now, this is more relevant and important question. How do we sort the given data? Given boxes of different sizes, a human brain with help of senses can sort them quickly manually. But, can we manually sort an array of 1 million numbers manually? Yes we can only if we have an year to do sorting. Otherwise, we will have to write a code and using an algorithm we can sort these numbers quickly and automatically. As for any given problem there can be many solutions, sorting can be done many different ways. Of course we will choose the best solution in the end, but, first we will have to see all the solutions before we come to any conclusion. So let’s begin.

Sorting algorithms can be mainly divided into two categories.

In-place or Internal Sorting : The sorting which does not require additional memory to perform sorting i.e. the memory required fits in to the main memory. Main algorithms within this category are
1. Selection Sort
2. Insertion Sort
3. Bubble Sort
4. Quick Sort
5. Heap Sort
Not in-place or External Sorting : The sorting which needs equal or more additional space than given data. Main algorithms within category are
1. Merge Sort*

* Note: Merge Sort can also be written in In-place code

So let’s see In place sorting algorithms..

Selection Sort

As the name suggests Selection Sort, this sorting algorithm selects the next value based on certain criteria. For example, if we are given numbers in an array it will choose the smallest number in all the array to place it in the 0th place by swapping original number at this place by the new number and then select the smallest amongst remaining numbers and place it in 1st place by swapping original number at this place with the newer smallest number and so on until we are left with the largest number that will automatically be placed at the end of the array. Let’s look at the pseudo code for this sorting algorithm.

Pseudo Code:

Let A be the array of N numbers which needs to be sorted
→For Index I from 0 to N-1 
    →Let Num be the number at Ith place 
    →For Index J from I to N-1 
        →Find A number Num1 which is smallest number within range of J (I to N-1) at jth place in the array 
            →Swap Num at Ith place with Num2 at jth place

Demonstration:

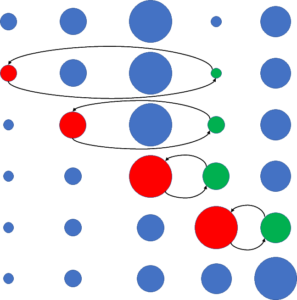
Take a look at following circles with random sizes. We will apply selection sort algorithm on them to demonstrate how this algorithm works mathematically. Red circle shows the Ith circle and green circle shows the smallest circle in the rest of the circles i.e. jth circle. These two circles get swapped and so on till the end. As you can see, the algorithm ‘selects’ smallest amongst remaining items and replaces with current one and does so till the end. Hence called selection sort.

Actual Code:

def SelectionSort(arr):
  tempId = 0;
  i = 0
  j = 0
  for i in range(0,len(arr)):
    tempVal = arr[i]
    tempId = i
    for j in range (i+1,len(arr)):
      if(arr[j] < tempVal):
        tempVal = arr[j]
        tempId = j
    temp = arr[i]
    arr[i] = arr[tempId]
    arr[tempId] = temp
  return arr

Pros:

Simple sorting algorithm to implement and understand
Will be very quick on an already sorted list

Cons:

Not so fast sort algorithm

Insertion Sort

This sorting algorithm is very simple to explain. Let’s think that, you are given some playing cards while playing Playing Cards. What’s the first thing that you do? Of course you, put lighter cards on the left and heavier on right. Do you know that you have used Insertion Sort!? Yes, how do you do this? You start from the left most card and move to right, if card on the right is lighter then we move it to left side, now even at this place current card is lighter than the left card then we move it to the left. We do it until playing cards in the hand are sorted completely. I will demonstrate this later on, first let’s look at the pseudo code for this sorting algorithm.

Pseudo Code:

Let A be the array of N numbers which needs to be sorted
→For Index I from 0 to N-1 
    →For Index J from I down to 0 
        →If NUM1 at (J-1)th place is smaller than Num at Jth place 
            →Swap number at Jth place with (J-1)th place

Demonstration:

What will be the the first step? Let’s move from left to right and swap the lighter card on the right with left card until the left card is lighter than current card. First card is 1 of hearts so we leave it. 6 of hearts is on the right of 8 of hearts. So, we swap these two cards. Now, we move further on right, 4 of hearts is on the right side of 8 of hearts, so we move 4 of hearts on the left to 8 of hearts. But, still 4 of hearts will be on the left of 6 of hearts so we will have to swap these two cards till the point, the card on the left of 4 of hearts is smaller. When we perform this step for each card we come up with Insertion Sort.

Actual Code:

def InsertionSort(arr):
  i = 0
  j = 0
  tempVal = 0
  for i in range(0,len(arr)):
    j = i 
    while(j > 0 and arr[j] < arr[j-1]):
      tempVal = arr[j]
      arr[j] = arr[j-1]
      arr[j-1] =  tempVal
      j = j - 1
    i = i + 1
  return arr

Pros:

Simple sorting algorithm to implement and understand in linear search
If a backwards linear search is used, it is much faster on an partially sorted array

Cons:

On an array, insertion sort is slow because all the elements after given element have to be moved

Bubble Sort

From the name of it, Bubble sort algorithm depicts the bubbles in liquid. Simply speaking, bigger sized bubble rises to the surface quickly than the smaller sized bubble. So, this sorting algorithm, takes the larger element more and more towards the end till the point where it can’t be moved because next element is larger than the current element. This is in place sorting algorithm. The code just has to look at the next element and has to decide whether there is a need for larger element to get swapped. This processes continues till all the larger elements are moved to the extremes until they can’t be moved further because there is a larger element than them up next. Let’s look at the pseudo code of this sorting algorithm.

Pseudo Code:

Let A be the array of N numbers which needs to be sorted
→While there is need of sorting to be performed i.e. NeedSorting is True 
    →Boolean NeedSorting is False 
    →For Index I from 0 to N-2 
        →If NUM1 at (I+1)th place is smaller than Num at Ith place 
            →Swap number at Jth place with (J-1)th place 
            →NeedSorting is True

Demonstration:

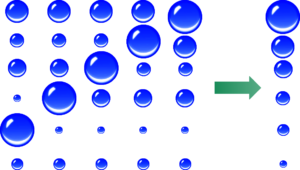
Let’s take a look at following image. These are bubbles floating randomly in a liquid! The left most column is the initial condition. The output of Bubble Sort is ultimately to have larger sized bubble on the top and the smallest at the bottom. We know the basic principle that, the larger bubble should rise and smaller bubble should get replaced with the larger one. In the image as we move from left to right, we move the larger bubble up by swapping with smaller bubbles, till the point there is no larger bubble on top of it. This is the first iteration. We continue to do the same in next iterations until all the bubbles get sorted out like the right most column.

Actual Code:

def BubbleSort(arr):
  temp = 0
  needSorting = True
  i = 0
  while(needSorting):
    needSorting = False
    for i in range(0,len(arr)-1):
      if(arr[i+1] < arr[i]):
        temp = arr[i]
        arr[i] = arr[i+1]
        arr[i+1] = temp
        needSorting = True
  return arr

Pros:

Simple sorting algorithm to implement and understand
Fairly faster on already sorted or partially sorted array

Cons:

Slowest of all sorting algorithms

Quick Sort

Tony Hoare in 1959 developed this sorting algorithm. This is a comparison sorting algorithm. In general this algorithm is faster than most of the algorithms, especially Heap Sort and Merge Sort (though theoretically Heap Sort is fastest). This algorithm works around the main component called Pivot. Given data data is divided into two sets where one set has all data lesser than pivot value and other one greater values. This algorithm continues on sub-dividing the halves till the point that smallest sub-division gets sorted. Ultimately sorting the whole data. This is an efficient sorting algorithm.

Pseudo Code:

Let A be the array of N numbers which needs to be sorted

PARTITION FUNCTION (Array, Start, End) 
    →Let Pivot be Array[LeftPos] Left = Start+1 Right = End Done Boolean be False initially 
    →While Done is False →While Left is equal or less than Right AND Array[Left] < Pivot 
        →Left = Left + 1 
    →While Array[Right] is greater than or equal to Pivot AND Right is greater than or equal to Left 
        →Right = Right - 1 
    →If Right lesser than Left 
        →Done = True 
    →Else 
         Swap Array[Left] and Array[Right] 
    →Swap Array[Start] and Array[Right] 
    →Return Right 

QUICKSORT FUNCTION (Array, Start, End) 
    →If Start is lesser than End 
        →Let Pivot = PARTITION(Array, Start, End) 
        →QUICKSORT(Array, Start, Pivot-1) 
        →QUICKSORT(Array, Pivot+1, End) 
    →Return Array

Demonstration:

If you can take a look at following image, we want to arrange people in ascending order w.r.t. their heights. So, let’s start sorting the people using Quick sort algorithm. The green one is the Pivot. We divide given people in two sets, shorter people on the left side and taller people on the right side by swapping their positions from original sequence. Now, let’s consider left set and now we will choose another pivot person and further divide this set where shorter ones will be on left and taller ones on the right. Same should be applied on the set on the right side. If we go on dividing and sub-dividing the given sets depending on the given pivot ultimately, we will end up with sorted data. And at end the sorting algorithm implementation we have sorted people according to their heights.

Actual Code:

#Partition Function
def partition(arr, start, end):
    pivot = arr[start]
    left = start+1
    right = end
    done = False
    while not done:
        while left <= right and arr[left] <= pivot: left = left + 1 while arr[right] >= pivot and right >=left:
            right = right -1
        if right < left:
            done= True
        else:
            # swap places
            temp=arr[left]
            arr[left]=arr[right]
            arr[right]=temp
    # swap start with arr[right]
    temp=arr[start]
    arr[start]=arr[right]
    arr[right]=temp
    return right

# Quick Sort Function	
def QuickSort(arr, start, end):
    if start < end:
        # partition the list
        pivot = partition(arr, start, end)
        # sort both halves
        QuickSort(arr, start, pivot-1)
        QuickSort(arr, pivot+1, end)
    return arr

Pros:

Extremely fast on average/ normal cases

Cons:

Tricky to implement and debug
Very slow in worst cases in real life
Bad implementation may cause stack overflow/ infinite loops

Merge Sort

John von Neumann invented this divide and conquer sorting algorithm in 1945. It is main competitor of Quick Sort algorithm in real life. Merge Sort is a comparison based sorting algorithm . The consecutive data will be compared with each other and swapped if needed. Merge Sort algorithm is mostly stable in real life. This algorithm is divides the given data to the smallest sorted element and then repeatedly merges all sorted subdivisions till we end up with whole data sorted out. Merge sort is implemented as in-place as well as not in-place sorting algorithms. In this article I will explain the algorithm but will provide in-place pseudo code.

Pseudo Code:

Let A be the array of N numbers which needs to be sorted

MERGESORT FUNCTION(Array)
    →Let Integer Mid = Length(Array)/2
     LeftHalf = Array[0..Mid]
     RightHalf = Array[Mid+1..N-1]
     
     MERGESORT(LeftHalf)
     MERGESORT(RightHalf)

     Let I, J, K all equal to Zero 0
     →WHILE I is lesser than Length(LeftHalf) AND J is lesser than Length(RightHalf)
         →IF LeftHalf[I] is lesser than RightHalf[j]
             →Array[K] equal to LeftHalf[I]
              I = I + 1
         →ELSE
             →Array[K] equal to RightHalf[J]
              J = J + 1
         K = K + 1
     →WHILE I is lesser than Length(LeftHalf)
         →Array[K] equal to LeftHalf[I]
          I = I + 1
          K = K + 1
     →WHILE J is lesser than Length(RightHalf)
         →Array[K] equal to RightHalf[J]
          J = J + 1
          K = K + 1
    →Return Array

Demonstration:

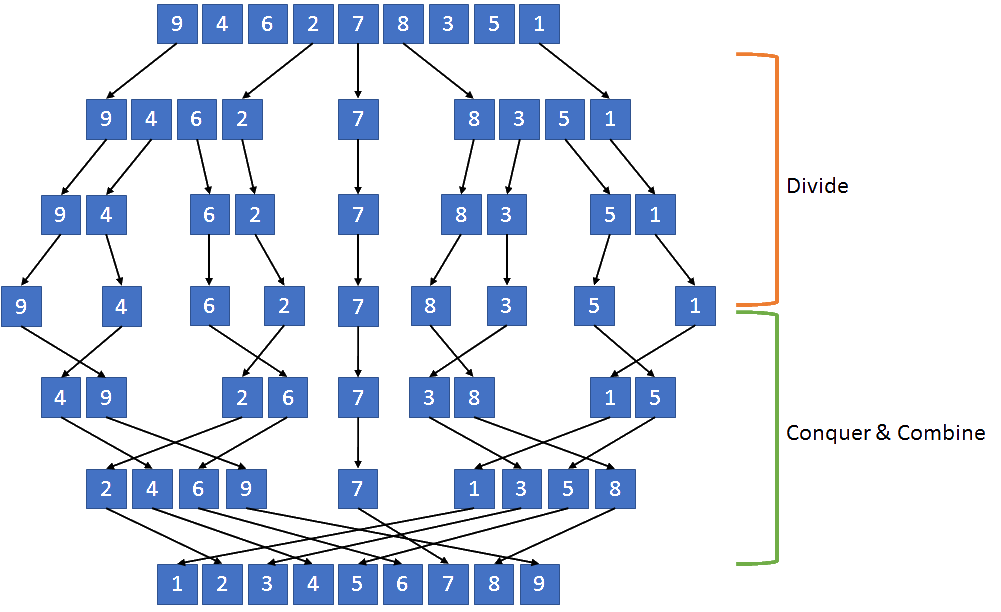
Following image shows how Merge Sort is implemented. In the first step 7 becomes the mid point. Given data is now divided in three parts. In the next steps these sets are divided and further divided, so that sub sets will have only one element at the end. One element is the smallest sorted element [9,4,6,2,7,8,3,5,1]. Now after dividing the data it’s time to conquer and combine the element is correct order by comparison [[4,9] , [2,6], [7], [3,8], [1,5]]. As you can see in the bottom half, sorting algorithm starts combining sub sets with proper order. Finally the sorted data is produced. This is how Merge sorting algorithm works.

Actual Code:

def MergeSort(arr):
  if len(arr)>1:
    mid = len(arr)//2
    lefthalf = arr[:mid]
    righthalf = arr[mid:]

    MergeSort(lefthalf)
    MergeSort(righthalf)

    i=0
    j=0
    k=0
    while i < len(lefthalf) and j < len(righthalf):
      if lefthalf[i] < righthalf[j]:
        arr[k]=lefthalf[i]
        i=i+1
      else:
        arr[k]=righthalf[j]
        j=j+1
      k=k+1

    while i < len(lefthalf):
      arr[k]=lefthalf[i]
      i=i+1
      k=k+1

    while j < len(righthalf):
      arr[k]=righthalf[j]
      j=j+1
      k=k+1
          
  return arr

Pros:

Constant performance O(n*log n) for all cases
Simpler to understand than Heap sort

Cons:

Slower than Quick Sort in average case
May require more memory in not in-place implementation

Heap Sort

Heap Sort algorithm is one of the most difficult sorting algorithms to understand. In a way it is (too much) modified Selection sort algorithm. Let’s first understand ‘Heap’

Heap:

Heap is a special tree based data structure. All nodes of Heap must satisfy following conditions.

Shape Property
- A Heap data structure must always be a complete binary tree. Which means each must have two children.
Heap Property
- All nodes are either greater than or equal to or less than or equal to each of its children.
- If the parent nodes are greater than their children, the Heap is called a Max-Heap, and if the parent nodes are smaller than their children nodes, the Heap is called Min-Heap.

Demonstration:

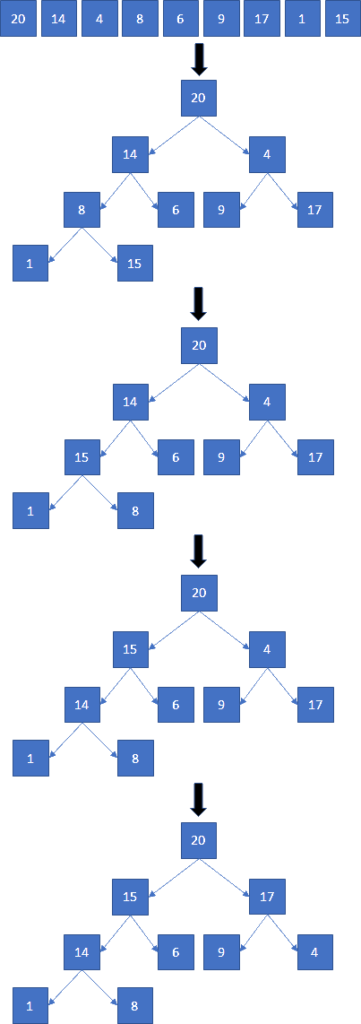
For Heap Sort algorithm it’s better to give the demonstration instead of pseudo code. Keep looking at the Block ’15’ and Block ’17’ and you will understand how heap is build.

Actual Code:

def heapify(arr, n, i):
    largest = i  # Initialize largest as root
    l = 2 * i + 1     # left = 2*i + 1
    r = 2 * i + 2     # right = 2*i + 2
 
    # Check if left child of root exists and is greater than root
    if l < n and arr[i] < arr[l]:
      largest = l
 
    # See if right child of root exists and is greater than root
    if r < n and arr[largest] < arr[r]:
      largest = r
 
    # Change the root node, if needed
    if largest != i:
      arr[i],arr[largest] = arr[largest],arr[i]  # swap

      # Heapify the root node.
      heapify(arr, n, largest)
 
# The main Heap Sort function to sort an array of given size
def HeapSort(arr):
  n = len(arr)

  # Build a maxheap. Please see the reference in the description
  for i in range(n, -1, -1):
    heapify(arr, n, i)

  # One by one extract elements from the hepyfied data
  for i in range(n-1, 0, -1):
    arr[i], arr[0] = arr[0], arr[i]   # swap .. advanced way to do swap in python
    heapify(arr, i, 0)
      
  return arr

Pros:

Constant performance O(n*log n) for all cases
Non recursive sort out of O(n*log n)performance sorting algorithms

Cons:

Slower than Quick Sort in average case
Difficult and lengthy in implementation

Shell Sort

Developed first by Donald Shell Shell sort algorithm at the core is technically a modified and efficient way of applying insertion sort. Shell Sort algorithm is an unstable algorithm.It’s just that instead of comparing each and every element with every other element, we take a specified gap and then compare those two elements. In this algorithm we start with largest possible gap and then lower the gap as we go on. This is a very fast sorting algorithm.

Pseudo Code:

Let A be the array of N numbers which needs to be sorted
SORTWITHGAP FUNCTION(array, start, gap)
    →LOOP I FROM start+SublistLength to Length(array) with step of gap
        →Let CurrentValue be equal to array[I]
         Let Position be equal to array I
            →WHILE Position is greater than or equal to gap AND array[Position-gap] is greater than Currentvalue
                →array[Position] be equal to array[Position-gap]
                 Position be equal to Position-gap
            →array[Position] be equal to CurrentValue

SHELLSORT FUNCTION(Array)
    →Let SublistLength = Length(Array)/2
    →WHILE SublistLength > 0
        →LOOP I FROM 0 to SublistLength
            →SORTWITHGAP(Array, I, SublistLength)
        →SublistLength = SublistLength/2

Demonstration:

Please take into account following given array. In the first iterate, the gap became length(array)/2 i.e. 4. And Shell sorting algorithm will compare every gap’th element and swap if needed. Then For next iteration, gap becomes 3 and so on. So, finally we end up with sorted array. I am not providing too many words for this sorting algorithm, I believe reader by now should have developed the way of interpretation of images and given number!

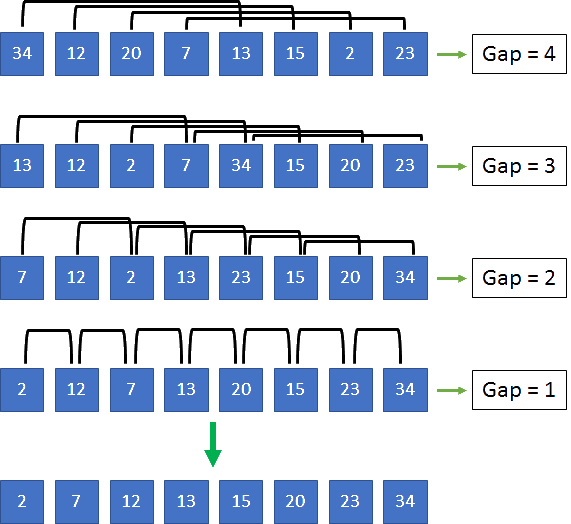
Actual Code:

def ShellSort(arr):
  sublistcount = len(arr)//2
  while sublistcount > 0:

    for startposition in range(sublistcount):
      SortWithGap(arr,startposition,sublistcount)

    sublistcount = sublistcount // 2
  return arr
  
  
def SortWithGap(arr,start,gap):
  for i in range(start+gap,len(arr),gap):

    currentvalue = arr[i]
    position = i

    while position>=gap and arr[position-gap]>currentvalue:
      arr[position]=arr[position-gap]
      position = position-gap

    arr[position]=currentvalue

Pros:

Efficient for medium-size lists

Cons:

Slightly tricky to implement and debug
Better performance than Selection, Insertion and Bubble Sorting algorithm but not as good as Quick Sort, Merge sort and Heap Sort algorithms

Sorting Algorithms Performances in Big O Notation

Performance Type	Worst	Best	Average	Worst Case - Space Complexity
Selection Sort	О(n^2)	О(n^2)	О(n^2)	О(n)
Insertion Sort	О(n^2)	О(n)	О(n^2)	О(n)
Bubble Sort	О(n^2)	О(n)	О(n^2)	O(1)
Quick Sort	О(n^2)	O(n log n)	O(n log n)	O(n)
Merge Sort	O(n log n)	O(n log n)	O(n log n)	О(n)
Heap Sort	O(n log n)	O(n log n)	O(n log n)	O(1)
Shell Sort	O(n(log2)^2 n)	O(n log n)	Depends on the gap O(n^1.25) from available literature	О(n)

Comparative analysis of performances in Sorting Algorithms in Big O notation in Worst, Best and Average cases. Also, Big notation for worst case space complexity. These are general Big O notations and not of any variants of the sorting algorithms

Million Dollars Question .. Which Sorting Algorithm to use?

This is the trickiest question asked for sorting algorithms. It is as difficult as which language is better C, C++, Python or Java? The short answer is, ‘it depends on the application’. Even if this is the answer some algorithms are surely better than others in all aspects. For example Quick Sort algorithm is better than Selection, Insertion and Bubble Sort. Merge Sort, Quick Sort and Heap Sort are strong competitors of each other but Heap Sort can be unstable. That’s why I say ‘it depends on the application’. I hope looking at the Pro’s and Con’s will make sure that you will choose the best sorting algorithm for you application. Best of luck.. keep learning.. keep sharing!

Appendix

Before, we conclude this article, I just want to share a small piece of code which was asked in interviews several times. It is vaguely similar to sorting algorithms. It’s reversing order of an array or a string. Of course, one can create a new array of the same size and can fill it up in a loop where I decrements from Length(Array)-1 to 0. But, this is an inefficient way of reversing the array because,

We end up using additional memory
After the loop we re-allocate the original array, which is heavy
Slower when the size of array is greater

So which’s the efficient way? Simple think of some boxes placed in random order. Now while reversing the order all we have to do is swap left most box with right most box. Then move on to next box from left and swap it with second to last box and so on till we reach middle or box in the middle.

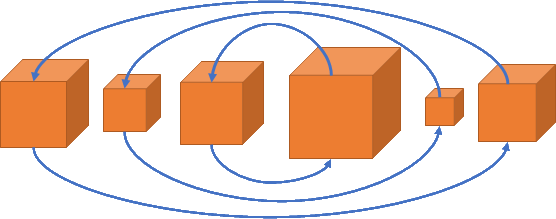
Pseudo Code:

Let A be the array of N numbers which needs to be reversed
→Let Left equal to 0 and Right equal to Length(A)-1
→WHILE Left is smaller than Right
    →Swap A[Left] and A[Right]
    →Left = Left + 1 and Right = Right + 1

Actual Code:

# Function to reverse a given string, here arr is actually a string like arr="Sample String"
def ReverseStringArray(arr):
  left = 0
  right = len(arr)-1
  arr = list(arr)
  while(left < right):
    temp = arr[left]
    arr[left] = arr[right]
    arr[right] = temp
    left = left + 1
    right = right - 1
  return ''.join(arr)

# Function to reverse a given numeric array  
def ReverseNumArray(arr):
  left = 0
  right = len(arr)-1
  while(left < right):
    temp = arr[left]
    arr[left] = arr[right]
    arr[right] = temp
    left = left + 1 
    right = right - 1 
  return arr

Interview Questions

Let’s see some interview questions that were either asked to me or my friends during their interviews. I would recommend if readers can also post any other interview questions in the comments section, so that others can benefit.

Q. Find the nth largest or smallest number in given array.

Answer:

Let’s consider Array as the given unsorted random array of numbers. Now to find nth largest or smallest number in the given array, first we will have to sort the array using some sorting algorithm. And then it becomes a simple job. If array is sorted in ascending order nth smallest number will be Array[n] and nth largest number will be Array[length(Array)-n]

Q. You are given large number video links which were viewed recently on the internet. Find top n most viewed videos.

Answer:

First of all we will have to create a class ‘Video’ which will have two properties as Link and Views, where Link is unique for each Video

class Video:
  Link = ""
  Views = 0

  def __init__(self, link):
    Link = link
    Views = 1

  def increamentView(self):
    Views = Views + 1

Then we iterate through the list of video links. Let’s also have an empty array which will hold ‘Unique‘ Videos with their links and views.

  GivenLinksArray #This is the given array of links
  UniqueVideosList = []
  
  def CreateNewOrAddViewsToVideo(link):
    found = false
    for v in UniqueVideoList:
      if v.Link == link:
        found = true
        v.increamentView()
    if found == false
      v = Video(link)
      UniqueVideosList.append(v)

  #Loop through given array of links and build UniqueVideosList
  def buildUniqueVideoList(Array):
    for link in Array:
      CreateNewOrAddViewsToVideo(link)

Now, once we have the array of Unique Videos, the next logical step is the Sort this unique videos array according to their views using the sorting algorithms we learned above. That’s the solution!

Q. A SEO system needs a function which can find 5 most frequently used words. Please write a code which will do that.

Answer:

It is actually similar to the answer of previous question. Every word is unique, so we can create a class Word with Spelling and Occurrence. And rest of the things are similar to the answer above.

Q. What is common between Quicksort and Selection Sorting Algorithm?

Answer:

Both sorting algorithms have Big O performance O(n^2) for worst cases

Q. In Selection Sort is it guaranteed that after N iterations we will have N sorted items in the list? Why?

Answer:

Yes. Because, on each iteration of selection sort, we make sure that the smallest or largest of the remaining list is chosen. Hence, it is guaranteed that after N iterations we will end up with N sorted items in the array.

Q. What is the worst case time taken by Heap Sort algorithm?

Answer:

O(n* log n)

Q. What is a stable Sorting Algorithm?

Answer:

Consider if there are two elements with same value at let’s say ith and jth position, where i < j in the given list . After sorting new places of these elements become mand n. If sorting algorithm ensures that ith element goes to mth position and jth element goes to nth position where, m < n then it is a stable algorithm.